Units: acfd=actual cfd, acfh=actual cfh, acfm=actual cfm, cfd=cubic foot per day, cfh=cubic foot per hour, cfm=cubic foot per minute, cfs=cubic foot per second, cm=centimeter, hr=hour, kg=kilogram, km=kilometer, lb=pound, m=meter, mm=millimeter, Mcfh=thousand cfh, MMcfd=million cfd, N/m2=Newton per square meter (same as Pascal), s=second, psi=pound per square inch, psia=psi (absolute), psig=psi (gage), scfd=std cfd, scfh=std cfh, scfm=std cfm, std=standard conditions (60F, 14.7 psia).
Introduction
The Weymouth, Panhandle A, and Panhandle B equations were developed to simulate
compressible gas flow in long pipelines. The Weymouth is the oldest and most common
of the three. It was developed in 1912. The Panhandle A was developed in the 1940s and
Panhandle B in 1956 (GPSA, 1998). The equations were developed from the fundamental energy
equation for compressible flow, but each has a special representation of the friction
factor to allow the equations to be solved analytically. The Weymouth equation is the most
common of the three - probably because it has been around the longest. The equations were
developed for turbulent flow in long pipelines. For low flows, low pressures, or short
pipes, they may not be applicable.
If the pressure drop in a pipeline is less than 40% of P1, then our Darcy-Weisbach incompressible flow calculation may be more accurate than the Weymouth or Panhandles for a short pipe or low flow. The Darcy-Weisbach incompressible method is valid for any flow rate, diameter, and pipe length, but does not account for gas compressibility. Crane (1988) states that if the pressure drop is less than 10% of P1 and you use an incompressible model, then the gas density should be based on either the upstream or the downstream conditions. If the pressure drop is between 10% and 40%, then the density used in an incompressible flow method should be based on the average of the upstream and downstream conditions. If the pressure drop exceeds 40% of P1, then use a compressible model, like the Weymouth, Panhandle A, or Panhandle B. You can always run all models and compare the results. The calculation is only valid for subsonic velocities. It does not check if velocities are sonic or supersonic.
Equations
The equations are shown below. The Weymouth, Panhandle A, and Panhandle B equations (GPSA,
1998; Crane, 1988) are the equation beginning with Qs=... with the
constants c, n, u, x, and y defined below. All of the equations shown below use the
English units indicated in the Variables section. Of course, our calculation uses a
variety of units with all of the unit conversions handled internally by the program.
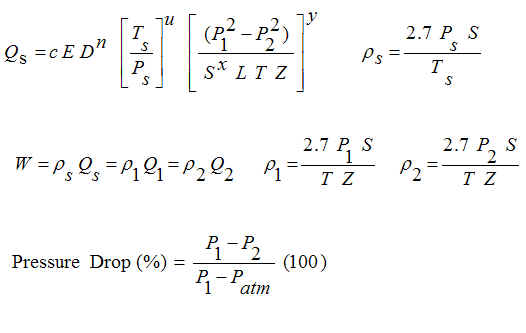
Variables
The units refer to the units that must be used in the equations shown above.
However, a variety of units may be used in our calculation.
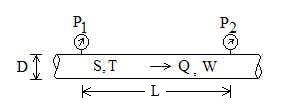
A = Pipeline cross-sectional area.
c = Constant. Weymouth: c=18.0625, Panhandle A: c=18.16125, Panhandle B: c=30.7083
D = Pipe inside diameter [inch].
E = Efficiency factor. Typically 0.85 to 1.0. The lower the number, the
rougher (or older) the pipe. Typical value is 0.92.
L = Pipeline length between locations 1 and 2 [mile].
n = Constant. Weymouth: n=2.6667, Panhandle A: n=2.6182, Panhandle B:
n=2.53
P = Absolute pressure in pipeline [psia, i.e. pounds per square inch absolute].
Q = Volumetric flowrate [cfh, i.e. cubic foot per hour]
S = Specific gravity of gas in pipeline, relative to air. That is, the ratio of the
gas's molecular weight to the molecular weight of air [unit-less].
T = Absolute temperature [Rankine]. Note: oR=oF+459.67
u = Constant. Weymouth: u=1.0, Panhandle A: u=1.0788, Panhandle B:
u=1.02
V = Velocity of gas = Q/A.
W = Mass flowrate [lb/hr, i.e. pounds per hour].
x = Constant. Weymouth: x=1.0, Panhandle A: x=0.853, Panhandle B: x=0.961
y = Constant. Weymouth: x=0.5, Panhandle A: x=0.5392, Panhandle B: x=0.51
Z = Gas compressibility. Value typically 1.0 at standard conditions. Typically
decreases as pressure increases. Can be as low as 0.4 or so. Exact computation
depends on make-up of the gas, gas critical pressure and temperature, and actual
temperature and pressure.
ρ = Greek letter rho. Density [lb/ft3, i.e. pounds per cubic
foot]. Note that the equation for ρs uses a value of 1.0 for the
compressibility.
Subscripts:
1 = Upstream conditions.
2 = Downstream conditions.
atm = Atmospheric conditions (14.73 psia).
s = Standard conditions (520 R, 14.73 psia)
Error Messages
"Need D>0", "Need L>0", "Need S>0", "Need
Qs>0", "Need W>0", "Need E,Z > 0".
These are initial checks. Diameter, length, specific gravity, and flows must be positive
numbers.
"Need T>0 K", "Need P1>0 absolute", "Need P2>0 absolute", "Need P1>P2". Temperature must be greater than absolute zero. Pressures must be greater than 0 absolute. And, pressure difference must be positive. Since you may have entered temperature in other units or pressure as gage, the calculation does some initial computations to determine the validity of the input.
"P1 too small". This message appears if P2 is computed as less than 0 absolute.
References
Crane Co. 1988. Flow of Fluids through Valves, Fittings, and Pipe.
Technical Paper 40 (TP-40).
GPSA (Gas Processors Suppliers Association). Engineering Data Book. 11ed. 1998.
© 2003-2025 LMNO Engineering, Research, and Software, Ltd. All rights reserved.
LMNO Engineering, Research, and Software, Ltd.
7860 Angel Ridge Rd. Athens, Ohio 45701 USA Phone: (740) 707‑2614
LMNO@LMNOeng.com
https://www.LMNOeng.com
